ODip – Optimal Diplomacy

Project Leader: Prof. Dr. Jörg Rambau
apl. Prof. Dr. Sascha Kurz
Prof. Dr. Rainer Hegselmann
Contact: Prof. Dr. Jörg Rambau

Project start: 2010/01/01

Project team:

• Prof. Dr. Jörg Rambau
  
• apl. Prof. Dr. Sascha Kurz
  
• Prof. Dr. Rainer Hegselmann
  

External partners:

Prof. Peter Hegarty, Chalmers University, Gothenburg, Sweden

Project description:

APPLICATION BACKGROUND

In philosophy and in social sciences a whole branch of research is concerned with the development of opinions over time and how they interact. In this project we ask what it means to "influence others" in this dynamical system. A strategy to state opinions in a sequence of committee meetings so as to convince as many members as possible is called a diplomacy. How can one compute or at least narrow down optimal diplomacies? What happens if not all informations about committee members are known to the diplomat? In order to interpret the formal results that our mathematical models produce, the Lehrstuhl Wirtschaftsmathematik (Prof. Dr. Jörg Rambau) cooperates in this project with the philosopher Rainer Hegselmann, Professor emeritus of the University of Bayreuth but still an active researcher with teaching activities in several renowned national and international institutions.

CONTRIBUTION TO THE MISSION OF MODUS

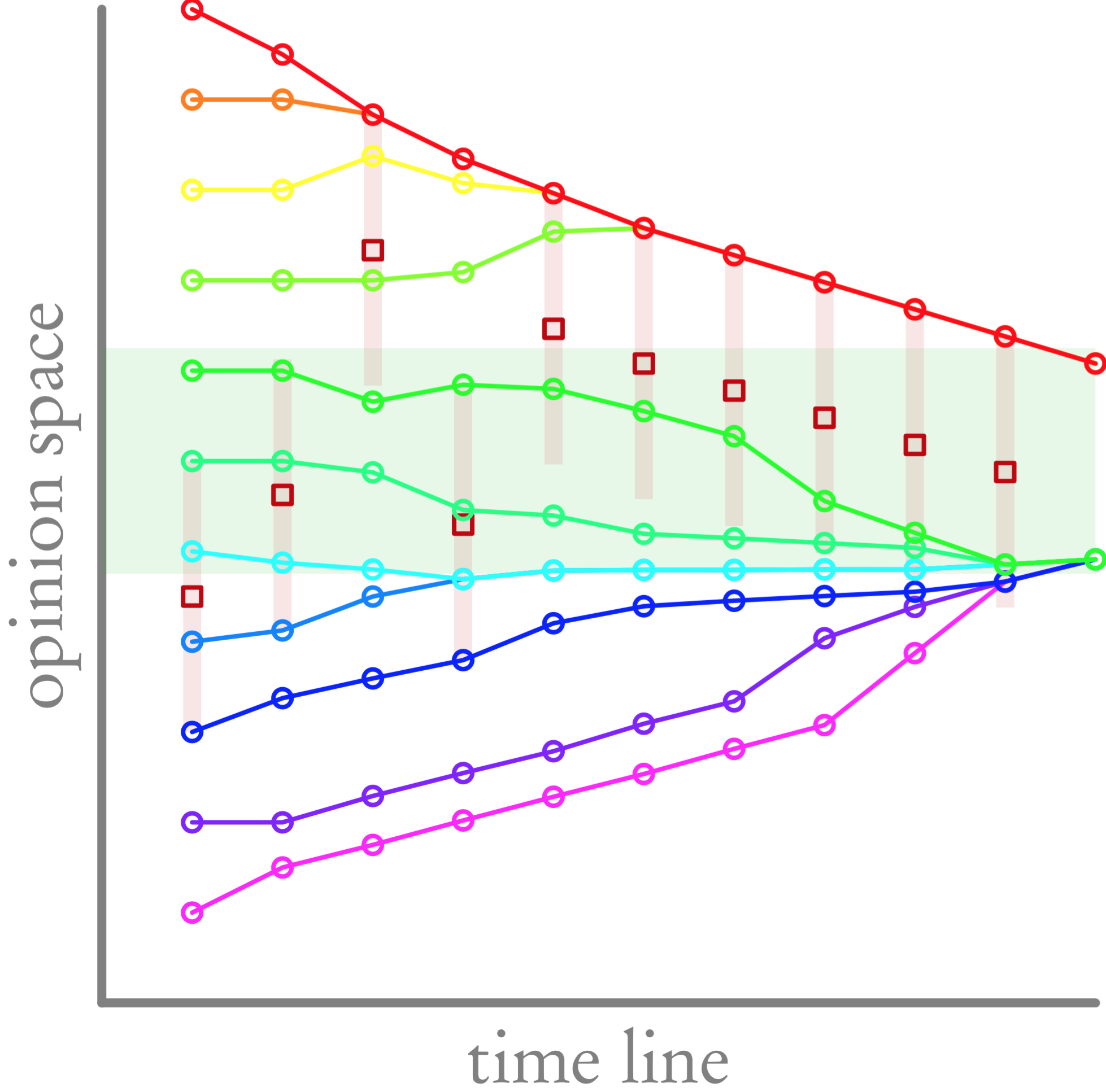
A widely accepted method to formalize all possible opinions is to assign a real or integral or binary number or vector to an opinion. All possible opinions encoded this way form the opinion space. One interaction principle is the bounded-confidence dynamics by Hegselmann and Krause from the late 1990s. It works for all sorts of metric opinion spaces. Each opinion is influenced by any other opinion that is at most a fixed distance apart from itself.  These not-to-far-away opinions are said to be in the confidence interval of an opinion. After a meeting, all opinions move to the average opinion in their respective confidence intervals. The formalization of influence is provided by an additional (or many additional) opinions that can be placed freely inside the opinion space by a controller. All other opinions cannot distinguish the controlled opinion from the other opinions, and the controlled opinion participates in the opinion dynamics as all other opinions do. The optimal control problem is to draw as many opinions as possible into a given set of the opinion space. An optimal control by stating best-possible opinions is called an optimal diplomacy. For one-dimensional opinion spaces, one can formally express this by mixed-integer linear programming models. In these models, the interaction configuration (who is in the confidence interval of whom) is indicated by binary variables, whereas the opinion positions in the opinion space are represented by real variables.

RESULTS

The project team, besides bringing up the problem and first models, has succeeded in presenting the best-so-far solutions for a benchmark problem with 11 members and 10 meetings. Several extensions are being investigated, e.g., to restrict diplomacies to consistent behaviour, cope with radicals that would not change their mind at all, or competing with other controlled opinions (game theory).